[Level5]하노이의 탑

문제

하노이의 탑은 대표적인 퍼즐의 일종입니다. 세 개의 기둥이 있고 맨 왼쪽의 기둥에는 원판의 크기 순서대로 N개가 쌓여 있습니다.

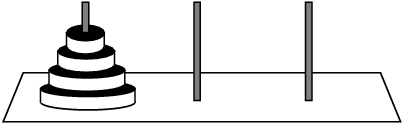
이렇게 쌓여 있는 원판을 가장 오른쪽 기둥으로 모두 옮겨야 합니다. 단, 한 번에 원판을 하나씩 이동시킬 수 있고, 큰 원판을 작은 원판 위에 쌓을 수 없습니다.

N개의 원판은 총 2N -1 번의 과정을 거쳐 이동할 수 있습니다. 하지만 어떠한 과정으로 원판을 옮겨야 2N -1 번만에 옮길 수 있는지는 아직 모릅니다. 원판이 N개 있을 때, Hanoi 함수에서 어떠한 과정으로 2N -1 번만에 옮길 수 있는지 과정을 리턴하세요.

리턴값의 표기 방법은 다음과 같습니다.

• 3개의 기둥은 순서대로 각각 1, 2, 3번으로 표기합니다.
• 원판을 기둥1에서 기둥3으로 이동했다면 [1, 3]으로 표기합니다.
• 원판을 기둥3에서 기둥1로 이동했다면 [3, 1]로 표기합니다.

이러한 이동 순서를 담는 배열을 리턴하면 됩니다. 예를들어 N이 2라면 아래 그림과 같이 옮길 수 있으므로

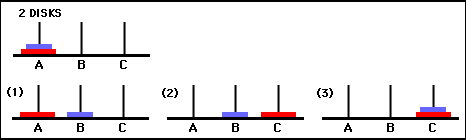
리턴값은 [ [1,2], [1,3], [2,3] ]입니다.

풀이 1

import java.util.Arrays;

class Hanoi {
  int count = 0;  

  public int[][] hanoi(int n) {
    // 2차원 배열을 완성해 주세요.    
    int num = (int)Math.pow(2,n)-1;		    
    int[][] answer = new int[num][2];

    move(1,2,3,n, answer);

    return answer;
  }

  public void move(int first, int center, int last, int n, int[][] answer){
    if(n==1){
    	count++;      
    }else{
      move(first, last, center, n - 1, answer);
      count++;
      move(center, first, last, n - 1, answer);
    }

    answer[count-1][0] = first;
    answer[count-1][1] = last;
  }

  // 아래는 테스트로 출력해 보기 위한 코드입니다.
  public static void main(String[] args) {
    Hanoi h = new Hanoi();
    System.out.println(Arrays.toString(h.hanoi(2)));
  }
}

알고리즘 단골 문제인 하노이의 탑이다. 학부생 시절에도 몇번 본 문제라 큰 문제없이 풀었다. 다만, 이 하노이의 탑 문제가 원하는 리턴값은 원판의 이동과정이라 처음에 봤을 땐 살짝 헤맸었다. 다시 생각해보니 그냥 2차원 배열에 이동경로를 재귀함수를 호출할 때마다 넣어주면 되는거라 해결되었다.

대부분 이런식으로 풀어서 특이한 풀이는 따로 보이지 않았다.